Fraunhofer-Institut für Algorithmen und Wissenschaftliches Rechnen SCAIDie dynamische Optimierung von Logistik- und Produktionsprozessen in Echtzeit steht ganz oben auf der Wunschliste vieler kleiner und großer Firmen. Man erhofft sich dadurch eine deutliche Kostenreduktion bei gleichzeitiger Verbesserung von Maschinenauslastung, Verteilung der Arbeitslast und Lieferzeiten von Produkten. Am Beispiel eines fiktiven Warenlagers lässt sich zeigen, welche Optimierungsmaßnahmen wie ineinander greifen und wie komplexe Prozesse schon für kleine Unternehmen handhabbar werden.
Optimierung von Logistik- und Produktionsprozessen –
am Beispiel der dynamischen Wegeoptimierung im Lager
Wie unterscheiden sich statische und dynamisch optimierte Lager?
Die Verwaltung eines modernen Lagers ist ein hochkomplexes Unterfangen. War es in der Vergangenheit oft ausreichend, das Lager gut zu strukturieren, statische Prozessabläufe klar zu definieren und genügend Lagerarbeiter zu beschäftigen, sind die Herausforderungen heute deutlich komplexer. Die Märkte sind globaler, große Versandunternehmen erweitern stetig ihr Netz an Logistik-Zentren – und die Kunden erwarten ein umfangreiches Sortiment und kurze Lieferzeiten.
Um erfolgreich und konkurrenzfähig zu bleiben, ist es notwendig, alle Abläufe effizient zu gestalten und dynamisch auf unvorhergesehene Ereignisse reagieren zu können. Dies erfordert eine genaue Analyse und Optimierung aller Arbeitsschritte im Lager. Die Minimierung von Lieferzeiten betrifft alle Prozesse, die die Kommissionierung eingegangener Bestellungen (Picking) beschleunigen. Hierzu gehören auf operativer Ebene vor allem das mögliche Zusammenfassen mehrerer Bestellungen (Batching) und die Wegeoptimierung (Routing).
Zudem können schon Entscheidungen in vorgelagerten Prozessen – etwa das Aufteilen des Lagers in verschiedene Produktbereiche (Zoning) oder die Strategie beim Einsortieren neuer Ware (Storage Allocation) – die Effizienz beim Picking entscheidend beeinflussen.
Zusätzliche Komplexität erwächst daraus, dass die einzelnen Optimierungsprobleme nicht getrennt voneinander betrachtet werden sollten, weil auch die Kombination verschiedener Strategien für unterschiedliche Probleme enormes Optimierungspotenzial birgt (van Gils, Ramaekers, Braekers, Depaire, & Caris, 2018).
Was lässt sich mit einer dynamischen Wegeoptimierung im Lager erreichen?
80% der Lager werden heute nach dem Picker-to-Part Muster betrieben.
50 Prozent der Arbeitsaufwände im Picker-to-Part-Lager entfallen auf Wege/Routen.
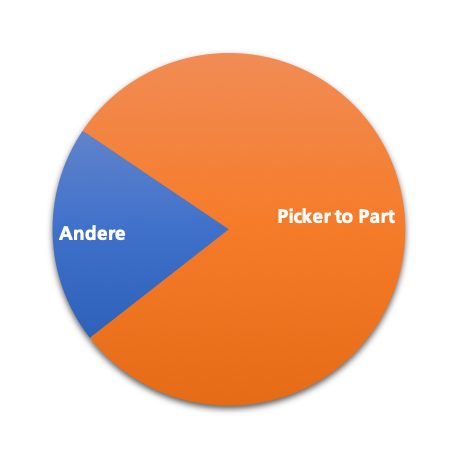
Heutige Lager in Westeuropa sind zu 80 Prozent sogenannte »Picker-to-Part«-Lager, in denen die Ware in Regalen einsortiert ist und beim Kommissionieren in einem manuellen Prozess von Lagerarbeitern gepackt wird (de Koster, Le-Duc, & Roodbergen, 2007). Auf das Picking entfallen in solchen Lagerhäusern bis zu 70 Prozent aller Arbeitsaufwendungen (Habazin, Glasnovic, & Bajor, 2017). Diese verteilen sich auf mehrere Arbeitsschritte, etwa die Entnahme der Ware oder das Erfassen von Warenbewegung im System.
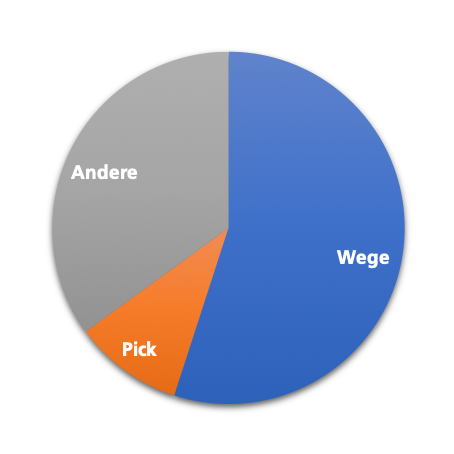
Das Ablaufen der Route ist mit ca. 55 Prozent der mit Abstand zeitintensivste Vorgang innerhalb des Pickings. Eine Verkürzung der Routen ermöglicht daher erhebliche Zeit- und Kosteneinsparungen.
Darüber hinaus hängen viele andere Prozesse im Lager davon ab, wie schnell einzelne Bestellungen kommissioniert werden können. Für den Zeitpunkt, zu dem eine Bestellung das Lager verlassen kann, ist entscheidend, in welcher Zeit die Bestellung zusammengestellt wird. Wird ein Auslieferungszeitpunkt verpasst, muss unter Umständen der gesamte Auslieferungsplan neu erstellt werden.
Für die Kunden ist es wichtig, bis zu welchem Zeitpunkt eine Bestellung abgegeben werden muss, damit sie noch am selben Tag das Lager verlässt. Auf kurzfristige Verspätungen bei Anlieferungen oder Ausfälle von Arbeitern kann außerdem besser reagiert werden, wenn das Picking weniger Zeit in Anspruch nimmt. Kurze Routen sparen also nicht nur Kosten, sie erhöhen auch die Flexibilität im operativen Betrieb sowie die Kundenzufriedenheit.
Kann man auch Wege optimieren?
Die naheliegende Herangehensweise, für jede eingegangene Bestellung die Positionen der bestellten Waren im Lager zu ermitteln und daraus die kürzeste Route zu berechnen, ist aus verschiedenen Gründen nicht ratsam. Zum einen ergibt sich, je nach Layout des Lagers, wie beim sogenannten Traveling Salesman Problem (TSP) möglicherweise ein NP-vollständiges Problem, dessen optimale Lösung nicht effizient berechnet werden kann. Selbst wenn eine Berechnung dieser Lösung möglich ist und sich eine optimale Route bestimmen lässt, kann diese Berechnung bei größeren Lagern sehr viel Rechenzeit in Anspruch nehmen. Sinnvoll ist daher der Einsatz heuristischer Ansätze, die effizienter in der Berechnung sind und ebenfalls sehr gute Lösungen liefern.
Ferner können meist deutlich kürzere Gesamtrouten erreicht werden, wenn mehrere Bestellungen zu einer Route zusammengefasst werden. Da sowohl Routing als auch Batching auf operativer Ebene auftreten, ist es naheliegend und vielversprechend, beide Probleme gemeinsam zu lösen. Für die simultane Berechnung von Batches und Routen existieren einige effiziente kombinierte Heuristiken (Cheng, Chen, Chen, & Jung-Woon Yoo, 2015) (Kulak, Sahin, & Taner, 2012) (Li, Huang, & Dai, 2016) (Lin, Kang, Hou, & Cheng, 2016).
Wie bereits einleitend erwähnt, müssen aber nicht nur das Routing und das Batching, sondern auch die Storage Allocation und das Routing gemeinsam betrachtet werden. Es lassen sich nämlich erheblich bessere Lösungen erzielen, wenn für die Entscheidung darüber, wo Ware eingelagert wird, und für die Bestimmung möglichst kurzer Routen aufeinander abgestimmte Heuristiken verwendet werden. Im folgenden Abschnitt wollen wir einen Eindruck davon vermitteln, welche Heuristiken hier zum Einsatz kommen können, wie die verschiedenen Heuristiken ineinandergreifen und welche Qualität die berechneten Lösungen haben.
Welche Heuristiken gibt es und wie gut sind die gelieferten Lösungen?
Verschiedene weitverbreitete Routing- und Storage-Allocation-Heuristiken (Within-Aisle, Across-Aisle, Peremiter)
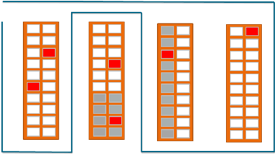
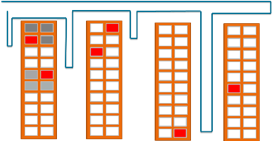
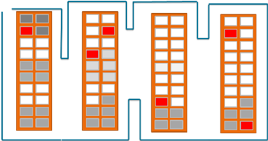
Wir nehmen hier der Einfachheit halber ein rechteckiges Lager mit mehreren parallelen Gängen an. Die Gänge können in beide Richtungen durchlaufen werden und sind auch breit genug, um wenden zu können. Ein Wechsel in einen anderen Gang ist nur am Ende der Gänge möglich. In der Praxis entscheiden derartige Eigenschaften eines Lagers darüber, ob eine Heuristik angewandt werden kann und wie gut ihre Lösungen sind. Wir beschränken uns hier auf einige wenige Heuristiken für Routing und Storage Allocation, die in der Praxis gute Ergebnisse liefern und bei denen das Potenzial im Zusammenspiel mit bestimmten Heuristiken der Storage Allocation besonders gut ersichtlich ist.
Bei der S-Shape-Heuristik durchläuft man jeden Gang, der auf der Route liegt, bis zum Ende und wechselt dort in den nächsten auf der Route liegenden Gang (vgl. die Route in der oberen Grafik).
Bei der Return-Heuristik läuft man das Lager nur an einer Seite ab. Dabei sammelt man in jedem Gang alle Güter ein und kehrt danach auf diese Seite zurück (vgl. die Route in der mittleren Grafik).
Bei der Largest-Gap-Heuristik geht man immer nur so weit in einen Gang hinein, bis die größte Lücke zwischen zwei einzusammelnden Gütern erreicht wird. Im letzten Gang wechselt man dann auf die andere Seite (vgl. die Route in der unteren Grafik).
Bei den Heuristiken für die Storage Allocation ist für den Ort der Lagerung der Produkte entscheidend, wie häufig sie bestellt werden. Bei der Within-Aisle-Heuristik werden die häufig bestellten Produkte in Gängen untergebracht, die näher am Depot liegen (vgl. die grauen Zellen in der mittleren Grafik).
Bei der Across-Aisle-Heuristik werden die häufig georderten Produkte an einer Seite des Ganges platziert (vgl. die grauen Zellen in der oberen Grafik).
Bei der Perimeter-Heuristik werden die häufig bestellten Produkte an beiden äußeren Seiten der Gänge gelagert (untere Grafik).
Weitergehende Möglichkeiten und Chancen
Obwohl es im Bereich der Lageroptimierung einige Standardsoftwarepakete gibt, zeigen die wissenschaftlichen Untersuchungen, dass die berechneten Ergebnisse nur dann gut sind, wenn sie auf die individuellen Abläufe und das Layout des jeweiligen Lagers zugeschnitten sind.
Es gibt zudem noch eine Vielzahl bislang nicht erwähnter Aspekte, die bei der Optimierung eine ebenso große Rolle spielen können. So kann die Strategie des Zoning bei größeren Lagern im Zusammenspiel mit dem Routing ebenfalls immense Auswirkungen haben. Die Anzahl der Lade- und Entladetore sowie die benutzten Transportgeräte müssen ferner ebenso berücksichtigt werden wie das Personal. Die operativen Entscheidungen beim Routing und Batching hängen dabei stark von der Anzahl der eingesetzten Lagerarbeiter ab. Sind mehrere Kommissionierer gleichzeitig im Lager unterwegs, werden optimale Ergebnisse nur dann erzielt, wenn mögliche »Staus« bereits in der Planung vermieden werden. Hier kann es dann durchaus sinnvoll sein, die ursprüngliche Strategie zu modifizieren. Kürzere Wartezeiten reduzieren nicht nur die Kommissionierzeit, sie erhöhen auch die Zufriedenheit der Arbeiter.
Berücksichtigt man all diese Aspekte, steht am Ende eine individuelle Optimierungslösung, die nicht nur Zeit und Geld spart, sondern auch Ressourcen schont sowie die Zufriedenheit der Kunden und Mitarbeiter erhöht.
Fraunhofer SCAI erarbeitet unter anderem im vom Bundeswirtschaftsministerium geförderten Projekt ERTRaWOS mit Partnern eine integrierte Lösung für Warenlager im Nahrungsmittelbereich. Dabei fließen die oben erwähnten und viele zusätzliche und nicht-intuitiv erfassbare Nebenbedingungen in die Optimierungslösung mit ein.
Diese Lösung entsteht mittels Nutzung einer neugeschaffenen Optimierungsplattform. Mit ihr bietet Fraunhofer SCAI die Grundlage für weitgehende maßgeschneiderte echtzeitfähige Optimierungslösungen in vielen Bereichen in der Logistik (bis hin zu 3PL und 4PL), in der Produktionsplanung (z.B. dem Scheduling von Maschinenbelegungen) und Supply-Chain Management. Alle diese Lösungen lassen sich häufig in eine bestehende Infrastruktur wie ein WMS und andere Werkzeuge integrieren.