Fraunhofer Institute for Algorithms and Scientific Computing SCAIThe dynamic optimization of logistics and production processes in real time is at the top of the wish list of many small and large companies in order to gain a significant reduction of costs while improving machine utilization, workload distribution and product delivery times. Using the example of a fictitious warehouse, it can be shown which optimization measures interlock with each other and how complex processes become manageable even for small companies.
Optimization of Logistics and Production Processes – Using the Example of Dynamic Route Optimization in Warehouses
What is the difference between static and dynamically optimized warehouses?
The management of a modern warehouse is a highly complex business. While in the past it was often sufficient to structure the warehouse well, to clearly define static process flows and to employ enough warehouse workers, today the challenges are much more complex. The markets are more global, large mail order companies are constantly expanding their network of logistics centers – and customers expect a wide range of products and short delivery times.
In order to remain successful and competitive, it is necessary to design all processes efficiently and to be able to react dynamically to unforeseen events. This requires a precise analysis and optimization of all work steps in the warehouse. The minimization of delivery times affects all processes that accelerate the picking of incoming orders. On an operational level, this includes above all the possible combination of several orders (batching) and route optimization (routing).
In addition, decisions in preceding processes – such as dividing the warehouse into different product areas (zoning) or the strategy for sorting new goods (storage allocation) – can have a decisive influence on picking efficiency.
Additional complexity arises from the fact that the individual optimization problems should not be considered separately, because the combination of different strategies for different problems also holds enormous optimization potential (van Gils, Ramaekers, Braekers, Depaire, & Caris, 2018).
What can be achieved by dynamic route optimization in the warehouse?
80% of warehouses today are operated according to the picker-to-part pattern.
50 percent of the workload in the picker-to-part warehouse is accounted for by distances/routes.
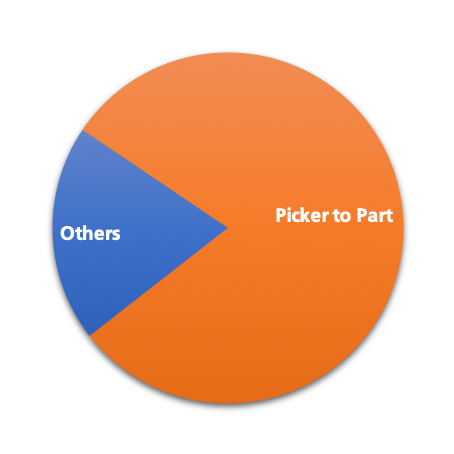
80% of today's warehouses in Western Europe are so-called "picker-to-part" warehouses, in which the goods are sorted on shelves and packed by warehouse workers in a manual process during picking (de Koster, Le-Duc, & Roodbergen, 2007). Picking accounts for up to 70 percent of all work in such warehouses (Habazin, Glasnovic, & Bajor, 2017). These are distributed over several work steps, such as picking the goods or recording goods movements in the system.
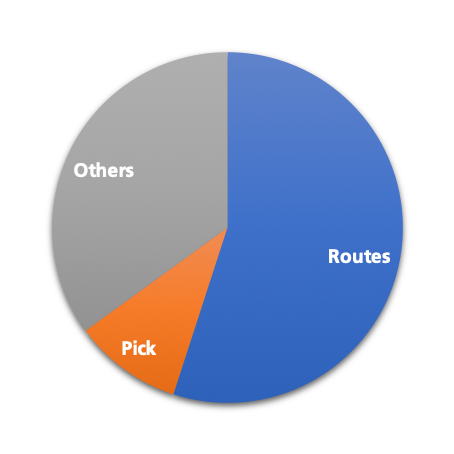
At around 55 percent, route processing is by far the most time-consuming process within the picking process. Shortening the routes therefore saves considerable time and money.
Furthermore, many other processes in the warehouse depend on how quickly individual orders can be picked. The time it takes for an order to leave the warehouse depends on how quickly the order is picked. If a delivery date is missed, the entire delivery schedule may have to be re-created.
It is important for customers to know by what time an order must be placed in order to leave the warehouse on the same day. Short-term delays in deliveries or absences of workers can also be dealt with better if picking takes less time. Short routes therefore not only save costs, they also increase flexibility in operations and customer satisfaction.
Can paths also be optimized?
The intuitive approach of determining the positions of the ordered goods in the warehouse for each received order and calculating the shortest route from there is not advisable for various reasons. On the one hand, depending on the layout of the warehouse, as in the case of the so-called Traveling Salesman Problem (TSP), an NP-complete problem may arise whose optimal solution cannot be calculated efficiently. Even if a calculation of this solution is possible and an optimal route can be determined, this calculation can take a lot of computing time for larger warehouses. Therefore it makes sense to use heuristic approaches, which are more efficient in the calculation and also provide very good solutions.
In addition, significantly shorter overall routes can usually be achieved by combining several orders into one route. Since both routing and batching occur at the operational level, it is obvious and promising to solve both problems together. For the simultaneous calculation of batches and routes, some efficient combined heuristics exist (Cheng, Chen, Chen, & Jung-Woon Yoo, 2015) (Kulak, Sahin, & Taner, 2012) (Li, Huang, & Dai, 2016) (Lin, Kang, Hou, & Cheng, 2016).
As mentioned in the introduction, not only routing and batching, but also storage allocation and routing must be considered together. This is because much better solutions can be achieved if coordinated heuristics are used to decide where goods are stored and to determine the shortest possible routes. In the following section, we want to give an impression of which heuristics can be used here, how the different heuristics interact and what quality the calculated solutions have.
Which heuristics do exist and how good are the delivered solutions?
Various widely used routing and storage allocation heuristics (Within-Aisle, Across-Aisle, Peremiter)
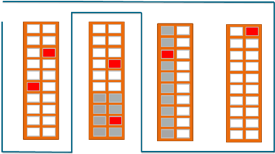
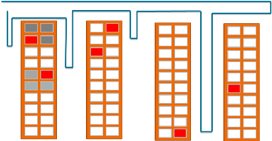
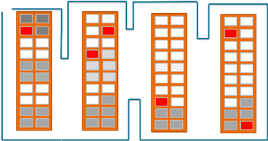
For the sake of simplicity, we assume here a rectangular warehouse with several parallel aisles. The aisles can be used in both directions and are wide enough to turn around. A change to another aisle is only possible at the end of the aisles. In practice, such properties of a warehouse decide whether a heuristic can be applied and how good its solutions are. We will confine ourselves here to a few heuristics for routing and storage allocation that deliver good results in practice and where the potential is particularly evident in interaction with certain heuristics of storage allocation.
With the S-Shape heuristics, you run through each aisle that lies on the route to the end and then switch to the next aisle lying on the route (see the route in the upper graphic).
In the Return heuristics, the bearing is only run on one side. You collect all goods in each aisle and then return to this side (see the route in the middle graphic).
In the Largest-Gap heuristics, you only go into one aisle until the largest gap between two goods is reached. In the last gear, you then switch to the other side (see the route in the lower graph).
In the heuristics for storage allocation, the location where the products are stored depends on how often they are ordered. In the Within-Aisle heuristics, the frequently ordered products are stored in aisles closer to the depot (see the gray cells in the middle graphic).
In Across-Aisle heuristics, the frequently ordered products are placed on one side of the aisle (cf. the gray cells in the upper chart).
In the Perimeter heuristics, the frequently ordered products are placed on both outer sides of the aisles (lower graph).
Further possibilities and opportunities
Although there are some standard software packages in the field of warehouse optimization, scientific research shows that the calculated results are only good if they are tailored to the individual processes and layout of the respective warehouse.
In addition, there are a number of previously unmentioned aspects that can play an equally important role in optimization. For example, the strategy of zoning in larger warehouses in combination with routing can also have immense effects. The number of loading and unloading gates and the transport equipment used must also be taken into account, as must the personnel. The operational decisions in routing and batching depend heavily on the number of warehouse workers employed. If several order pickers are on the road in the warehouse at the same time, optimal results are only achieved if possible »traffic jams« are already avoided in the planning stage. In this case, it can make sense to modify the original strategy. Shorter waiting times not only reduce picking time, they also increase worker satisfaction.
If all these aspects are taken into account, the result is an individual optimization solution that not only saves time and money, but also conserves resources and increases customer and employee satisfaction.
Fraunhofer SCAI is working with partners on an integrated solution for warehouses in the food sector, for example in the ERTRaWOS project funded by the German Federal Ministry of Economics. The above-mentioned and many additional and non-intuitively detectable constraints are incorporated into the optimization solution.
This solution is generated by using a newly created optimization platform. With this platform, Fraunhofer SCAI offers the basis for largely customized real-time-capable optimization solutions in many areas of logistics (up to 3PL and 4PL), production planning (e.g. scheduling of machine occupancy) and supply chain management. All these solutions can often be integrated into an existing infrastructure such as a WMS and other tools.