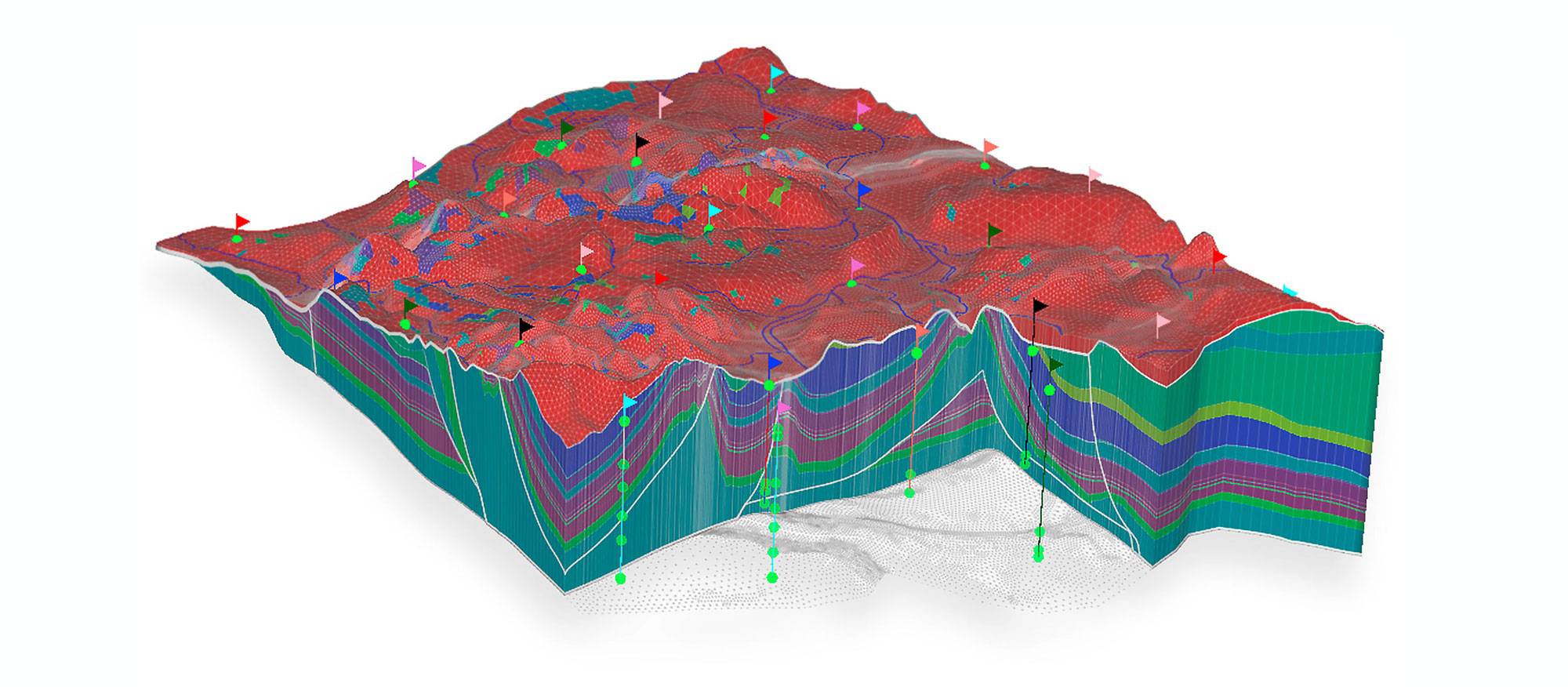
»SAMG has been the key to improving both the robustness and performance of our General Purpose Research Simulator – GPRS. With SAMG as the workhorse linear solver, we now routinely solve problems that were simply beyond our reach. SAMG is indispensable for reservoir flow simulation of large-scale, highly heterogeneous, unstructured reservoir models.«
Prof. Hamdi Tchelepi, Petroleum Engineering Department, Stanford University
»For our applications, SAMG is the fastest solver in the world. SAMG has enabled us to tackle large problems faster than ever before and attempt larger problems that were ever possible – for the first time we can make multi-million cell simulations routine where we properly capture the reservoir structure.«
Prof. Martin Blunt, Petroleum Engineering, Imperial College
(Translated from German:)»My congratulations to the very good product SAMG. It could provide what it promised – an experience that not always granted today.«
Prof. H.-J. G. Diersch, WASY GmbH, Berlin
»Experience has indicated that .... execution times ..... are typically 2 to 25 times faster than execution times using MODFLOW‘s PCG2 Package .....«
User Guide to the LMG Package, US Geological Survey, Boulder, Colorado
»SAMG is in a world of its own when it comes to linear solvers. It is robust, fast, and easy to implement on any platform, and has given our company a clear competitive edge. It has been a reliable work requiring little or no maintenance, allowing us to concentrate on our core business. Small or big, simple or complex, sparse or full, structured or unstructured – SAMG will solve it. Anybody contemplating using a linear solver need look no further than SAMG and its friendly and helpful author, Dr. Klaus Stueben.«
Marco Thiele, co-founder & President StreamSim Technologies